Our Network
Resources and Tools
Project-Based vs. Problem-Based Learning: Which is Right for Your Math Classroom?
Introduction to PBL
Project-based learning (PBL) is an inquiry-based and learner-centered instructional approach that immerses students in real-world projects that foster deeper learning and critical thinking skills.
In contrast to traditional instruction and rote memorization, project-based learning encourages learner agency, collaboration, and problem-solving, empowering students to become active participants in their own learning. Students collaborate to solve real world problems that require understanding content knowledge, critical thinking, creativity, and robust communication skills.
New Tech Network (NTN) schools employ a pedagogy of project-based learning and in math, this can result in enhanced student understanding by having learners make real-world connections to math content and skills. However, it can be difficult to do math on a deep level encompassing all the requisite mathematical standards. As a result, NTN strongly promotes primarily problem-based learning (PrBL) in math classrooms, although, at times there may be authentic ways to embed math in a project-based learning unit.
In this article we will highlight New Tech Network’s lens on PrBL, the similarities and differences between project-based learning and problem-based learning, and what both look like when implemented in the classroom.
What is Project-Based Learning (PBL)?
The basic principle of the project-based instruction lies in students actively participating in an authentic challenging problem that enables students to have experiential learning, connection to community members, higher classroom engagement, and a deeper understanding of content. The PBL approach diverges from traditional instruction by encouraging students to learn about and try to solve real world issues, use problem solving skills, communicate ideas, become proficient in technology tools, and make a personal connection to content. These skills prepare students for success in college and career.
To learn more about implementing project-based learning, project design, and project-based learning examples, explore the article: The Comprehensive Guide to Project-Based Learning: Empowering Student Choice through an Effective Teaching Method. For a more in-depth look at the benefits of project-based learning, read How Project-Based Learning is Effective in Education.
What is Problem-Based Learning (PrBL)?
Like project-based learning (PBL), problem-based learning (PrBL) engages students in complex tasks, employs student-centered instruction and small group work, and positions the teacher as a facilitator of learning. In addition, PrBL accurately reflects the types of explorations, discussions, questions, and interactions that are authentic to mathematics as a discipline. PrBL uses formative and performance-based assessments to give feedback and check student progress.
The key differences between project-based learning and PrBL are that PrBL focuses on one or two standards at a time and each problem takes place over a shorter time period (roughly one to four days). In PrBL, students are mainly exploring and discussing mathematical ideas, with an emphasis on the problem solving process and productive struggle, whereas in PBL there is a greater emphasis on creating a culminating product that answers a Driving Question.
Project-Based Learning vs Problem-Based Learning
NTN suggests a secondary math learning environment which utilizes problem-based learning (PrBL) and in elementary math, problems appear alongside projects and, when applicable, within a project-based learning curriculum.
Problem-based learning provides a rich problem solving environment that allows for and necessitates the learning and assessment of the New Tech Network Learning Outcomes of Agency, Written Communication, Oral Communication, Collaboration, and Knowledge and Thinking along with important content standards. There some key differences between project-based learning and problem-based learning, primarily in timing and scope, but far more similarities exist than differences as shown below:
Problem-Based Learning
-
Standards: 1-2 Standards
-
Time: 1-4 Days
-
Main Activity: Inquiry and Discourse
-
Emphasis: Problem-solving Process
Similarities
-
Engages students in complex tasks
-
Student-centered small-group work
-
Reflects the work of the discipline
-
Teacher as facilitator of learning
-
Formative and performance-based assessment
Project-Based Learning
-
Standards: 4+ Standards
-
Time: 4-6 Weeks
-
Main Activity: Applying Learning
-
Emphasis: Product
The Differences:
The easiest answer to the PBL vs PrBL question is scope. NTN often supports schools and districts in a project-based learning environment, which can cause a tricky situation in terms of scaling this to a problem or choosing to do a project. Projects are typically designed to learn about a larger cluster of standards that can be taught using a single context, warrant multiple weeks of learning, and culminate in a substantial product as a presentation of learning.
However, a project is often not sufficient to adequately develop the deep understanding required of some math concepts. This is where PrBL plays a key role. PrBL allows a teacher to scale down to focus on just a few standards and to focus on students’ processes as they tackle contextual scenarios over the course of a few problems while still enabling a real world application.
The Similarities:
There are far more similarities between PrBL and PBL than differences. Both project-based learning and problem-based learning include entry events, knows and need to knows, rubrics, etc. However, as the number of standards and duration is scaled down, entry events and rubrics must be scaled down as well. But while perhaps a bit shorter/quicker in a problem rather than project, we must not lose the intent of each similarity. Here are two examples to better illustrate this point.
Keeping the Intent of Entry Events and Knows and Need to Knows in PrBL
An entry event is the student introduction or “hook” to the project or problem. A well-crafted entry event will solicit student needs to be met in order to adequately address the content and skills presented in the project or problem’s plan. For a project, the introduction needs to kick off (and help to sustain) weeks of learning. Examples of entry events might include field trips, interview with community partners, or perhaps a debate.
Moving to PrBL, the purpose of the entry event remains the same, but the scale needs to shift. For a problem you might present students with text, an image, or a video that will prompt students to pose questions. This can be something as simple as the image at right of a restaurant promotion, as long as you can then prompt students what questions they have, and what additional information they need.
You’ll want to document these questions in some way, but note that in a problem the number of questions or “need to knows” will likely be fewer than for a project due to the scope of standards you’re addressing. Gather enough questions to allow students to have direction (know what they are starting to solve) and can begin to struggle in solving the problem.
Keeping the Intent of Rubrics in PrBL
As a problem scales down the number of standards you’re addressing, so too should you scale down the number of indicators you’re giving feedback around and assessing.
While the culminating product of a project often serves as a hefty assessment through a hefty rubric, a problem-based approach offers a teacher the opportunity to get really specific about the rubric indicators they are after, sometimes narrowing down to just 1 or 2 for a product. Similarly, PrBL teachers will need to narrow the focus of rubric indicators for the other New Tech Network Learning Outcomes.
For example, for collaboration you may also want to zoom in on just one or two indicators – few enough that you can authentically teach, provide feedback, and assess in the shorter time span of a problem.
New Tech Network's Problem-Based Learning Model
Problem-based learning as we think about it at NTN consists of three phases: Launch, Explore, and Discuss. Launch-Explore-Discuss allows students to engage in inquiry, build their self-regard, and have discourse in small and large groups.
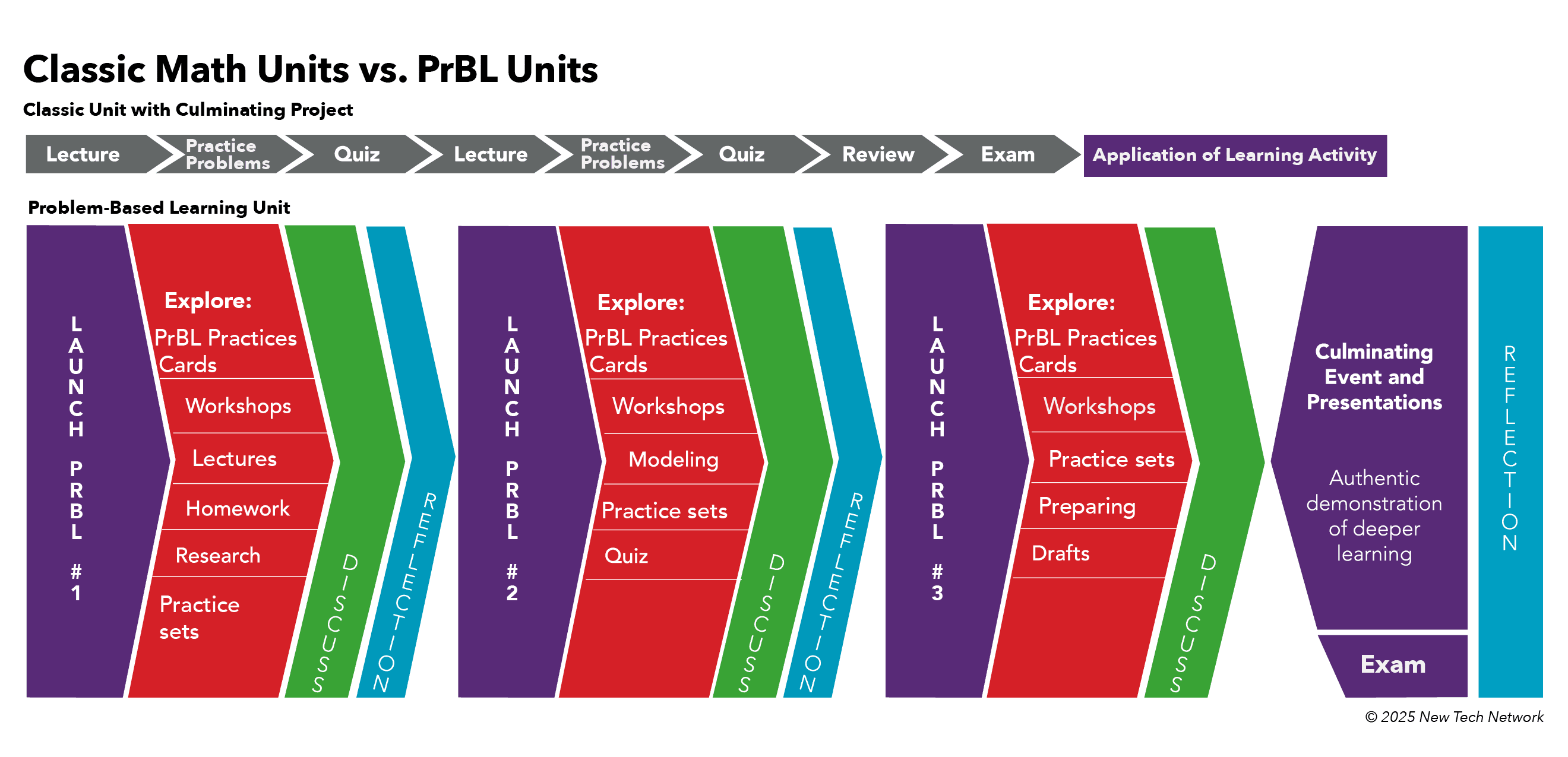
In Launch, students are introduced to the problem in a learner-centered way. Explore is when learners have time to explore solution strategies (correct or incorrect) in small groups, asking questions of each other and you. The problem ends with a Discussion in which multiple strategies are shared by learners and the whole class makes connections between different strategies, puts formal vocabulary to their ideas, and makes generalizations to connect to math standards. Each phase is discussed more in depth below.
Launch:
A problem-based lesson would begin with a launch, where the problem is introduced in a learner-centered way to support learners in making sense of the problem and what is being asked as well as building excitement and interest. In order for learners to engage meaningfully in a cognitively challenging task, they need time to process and make sense of the problem.
A key aspect of the launch is not to “get learners started” by showing the first step or an example problem. The goal and the teacher’s role is to spark inquiry, maintain productive struggle, and allow learners to pursue multiple solution strategies.
Explore:
The next phase is “explore”, where learners have time to try potential solution strategies that may or may not be correct in pairs or small groups, asking questions of each other and of the teacher. This phase serves to create a math classroom centered on student thinking and ideas, by giving students time to come up with their own solution strategies.
Facilitators must lean into their role as facilitators vs “rescuers”, moving away from the idea of saving students by telling them what to do. It’s okay if some of them are wrong, as there will be time to revise during the discussion section. This is also a time for learners to practice their collaboration and discourse in a low stakes setting.
Discuss:
Finally, all students engage in a whole-class discussion. During this time, learners share strategies, make connections, and generalize a rule. This is a time to share academic vocabulary, formal notation, and make explicit connections to prior topics and standards. After having time to come up with strategies in “explore”, students can compare multiple strategies and collectively decide what works and what doesn’t.
By drawing connections between strategies, learners can strengthen and deepen their understanding of the content. Teachers support learners during discussion by making connections and giving formal language and notation to learner generated ideas.
These strategies are not always easy to implement. Students need to be taught how to problem solve independently, how to work collaboratively in a group, and how to understand, evaluate, and question others’ ideas. These skills are supported by cultivating and sustaining a supportive and inclusive classroom culture. In addition to a strong classroom culture, facilitators must also consider important shifts in math instruction.
Key shifts in Math encouraged in a PrBL classroom
Math classrooms enacting these shifts provide a rich problem-solving environment that allow for and necessitate the learning and assessment of the New Tech Network Learning Outcomes. The Key Shifts in math facilitation are meant to guide the ongoing, hard work of all New Tech Network (NTN) math facilitators, new or veteran. We don’t pretend that they are easy; in fact, they often run directly against how we were taught to teach or even how we were taught ourselves and take years to fully implement.
Longtime methods of presenting and practicing content, and the associated frustration of students and teachers alike, are familiar to many of us. With these shifts as a lens, we can all work to reduce math anxiety, restore student engagement, and connect to the beauty of the subject we teach.
NTN Secondary Math Key Shifts
Successfully Supporting All Students
Key Shift One: Emphasis on Self Regard
Key Shift Two: Emphasis on Discourse
Key Shift Three: Emphasis on Inquiry
Key Shift #1: Improve Mathematical Self-Regard
It’s important for a teacher to communicate explicitly that each of their students are budding mathematicians. This directly contradicts deeply embedded cultural messages about who is “good at math” and what it means to be good at math (Boaler 2016). As a result, teacher messages must be intentional and consistent, as well as paired with a more accurate depiction of mathematics that aligns with the discipline, rather than the way mathematics is traditionally presented in schools.
For example, in the discipline, deep thinking, questioning, and creativity are key aspects of mathematics. However, in schools math classes tend to emphasize speed, breadth, and passive learning (Banilower et al. 2006).
By presenting mathematics as a discipline that requires a wider variety of skills, more students can see themselves as members of a mathematical community (Horn 2012). This also allows students of many cultural backgrounds to use their assets to be successful in mathematics (Carpenter et al. 1989).
Key Shift #2: Emphasis on Discourse
Research shows that complex knowledge such as mathematics is learned through social interactions (Vygotsky and Cole 1978; Lave and Wenger 1991). In traditional US math classrooms, discussion is typically teacher-led and consists of short, fact based questions and answers (Horn 2012).
The shift is to transform those discussions into ones that are student-led and consist of students’ conceptual ideas, questions, and mistakes, evaluating their own and others’ ideas.
Like all the shifts, this is not easy to accomplish and requires explicit instruction and support for students to learn how to participate in a small group or whole class discussion. In addition, it requires a change to class structures and the types of problems that are presented. Both must make space for student discussion and ideas to drive their own learning.
Key Shift #3: Emphasis on Inquiry
In an inquiry-based classroom, students construct their own knowledge, rather than teachers transferring knowledge to students. In this setting, the teacher’s role is to create a learning environment in which students can come up with ideas, share them, and refine them together with each other and the teacher (NCTM 2015).
One challenge is that teachers must maintain the cognitive load of the task – where students are engaging in reasoning and problem solving without being given a specific path to follow.
While these shifts are challenging, they are also mutually reinforcing. Inquiry and discourse position students as the possessors and creators of knowledge, which increases their self regard as mathematicians.
A learning environment that encourages inquiry will also lead to discussion as students come up with ideas, share them, and refine them in pursuit of understanding. As students come to regard themselves as mathematicians, they will feel more empowered to engage in discourse and PrBL.
PrBL Examples and Resources
Squirrel Race Guy is an Algebra 1 problem, designed in NTN’s Problem Planning Form and models the Explore-Launch-Discuss model described above. The planning form also includes a page that models the anticipatory planning required to design and implement strong problems.
Designing a 3D Product in 2D: Sports Bag This 7th grade sample problem is from the Mathematics Assessment Project which is part of the Math Design Collaborative initiated by the Bill & Melinda Gates Foundation. The project set out to design and develop well-engineered tools for formative and summative assessment that expose students’ mathematical knowledge and reasoning, helping teachers guide them towards improvement and monitor progress.
The Class Trip is a sample 3rd grade problem from Illustrative Math that models high-quality k-12 math problems aligned to NTN’s model of PrBL.
Resources for finding Math Problems to Adapt is a comprehensive list of resources curated by NTN for designing and adapting problems in your PrBL classroom.
Conclusion
Project-Based Learning is uses a real-world approach that requires students to use collaboration, problem solving and critical thinking skills that leads to a culminating product over an extended period of time. While Problem-Based Learning uses those same skills and narrows the focus to 1 or 2 standards over a shorter time period, emphasizing inquiry, exploration, and discussion of math concepts. Both approaches involve essential elements such as entry events that “hook” students with a real world problem or real math work and using rubrics for assessing learning outcomes.
New Tech Network’s Problem-Based Learning Model outlines three phases: Launch, Explore, and Discuss. Each phase plays a crucial role in engaging students in inquiry, building self-regard, and fostering discourse.
Both project-based learning and problem-based learning are both effective educational approaches that empower students to become active learners, critical thinkers, and effective collaborators. Using the resources from this article and creating a curriculum supported by projects and problems will allow students to strengthen their skills most needed for success in the 21st century.
About New Tech Network
New Tech Network is committed to meeting schools and districts where they are and helping them achieve their vision of student success. For a full list of our additional paths to impact or to speak with someone about how the NTN Model can make an impact in your district, please send an email to inquiry@newtechnetwork.org.
